Eigenmodes of a Cylinder

Note

The files for this example can be found in the examples/cylinder/ directory of the Palace source code.

Cavity

This example demonstrates Palace's eigenmode simulation type to solve for the lowest frequency modes of a cylindrical cavity resonator. In particular, we consider a cylindrical cavity filled with Teflon ($\varepsilon_r = 2.08$, $\tan\delta = 4\times 10^{-4}$), with radius $a = 2.74\text{ cm}$ and height $d = 2a$. From [1], the frequencies of the $\text{TE}_{nml}$ and $\text{TM}_{nml}$ modes are given by

\[\begin{aligned} f_{\text{TE},nml} &= \frac{1}{2\pi\sqrt{\mu\varepsilon}} \sqrt{\left(\frac{p'_{nm}}{a}\right)^2 + \left(\frac{l\pi}{d}\right)^2} \\ f_{\text{TM},nml} &= \frac{1}{2\pi\sqrt{\mu\varepsilon}} \sqrt{\left(\frac{p_{nm}}{a}\right)^2 + \left(\frac{l\pi}{d}\right)^2} \\ \end{aligned}\]

where $p_{nm}$ and $p'_{nm}$ denote the $m$-th root ($m\geq 1$) of the $n$-th order Bessel function ($n\geq 0$) of the first kind, $J_n$, and its derivative, $J'_n$, respectively.

In addition, we have analytic expressions for the unloaded quality factors due to dielectric loss, $Q_d$, and imperfectly conducting walls, $Q_c$. In particular,

\[Q_d = \frac{1}{\tan\delta}\]

and, for a surface resistance $R_s$,

\[Q_c = \frac{(ka)^3\eta ad}{4(p'_{nm})^2 R_s} \left[1-\left(\frac{n}{p'_{nm}}\right)^2\right] \left\{\frac{ad}{2} \left[1+\left(\frac{\beta an}{(p'_{nm})^2}\right)^2\right] + \left(\frac{\beta a^2}{p'_{nm}}\right)^2 \left(1-\frac{n^2}{(p'_{nm})^2}\right)\right\}^{-1}\]

where $k=\omega\sqrt{\mu\varepsilon}$, $\eta=\sqrt{\mu/\varepsilon}$, and $\beta=l\pi/d$.

The initial Gmsh mesh for this problem, from mesh/cavity_prism.msh, is shown below. We use quadratic triangular prism elements. There are also two other included mesh files, mesh/cavity_tet.msh and mesh/cavity_hex.msh, which use curved tetrahedral and hexahedral elements, respectively.

There are two configuration files for this problem, cavity_pec.json and cavity_impedance.json.

In both, the config["Problem"]["Type"] field is set to "Eigenmode", and we use the mesh shown above. The material properties for Teflon are entered under config["Domains"]["Materials"]. The config["Domains"]["Postprocessing"]["Energy]" object is used to extract the quality factor due to bulk dielectric loss; in this problem since there is only one domain this is trivial, but in problems with multiple material domains this feature can be used to isolate the energy-participation ratio (EPR) and associated quality factor due to different domains in the model.

The only difference between the two configuration files is in the "Boundaries" object: cavity_pec.json prescribes a perfect electric conductor ("PEC") boundary condition to the cavity boundary surfaces, while cavity_impedance.json prescribes a surface impedance condition with the surface resistance $R_s = 0.0184\text{ }\Omega\text{/sq}$, for copper at $5\text{ GHz}$.

In both cases, we configure the eigenvalue solver to solve for the $15$ lowest frequency modes above $2.0\text{ GHz}$ (the dominant mode frequencies for both the $\text{TE}$ and $\text{TM}$ cases fall around $2.9\text{ GHz}$ frequency for this problem). A sparse direct solver is used for the solutions of the linear system resulting from the spatial discretization of the governing equations, using in this case a fourth-order finite element space.

The frequencies for the lowest-order $\text{TE}$ and $\text{TM}$ modes computed using the above formula for this problem are listed in the table below.

$(n,m,l)$	$f_{\text{TE}}$	$f_{\text{TM}}$
$(0,1,0)$	––	$2.903605\text{ GHz}$
$(1,1,0)$	––	$4.626474\text{ GHz}$
$(2,1,0)$	––	$6.200829\text{ GHz}$
$(0,1,1)$	$5.000140\text{ GHz}$	$3.468149\text{ GHz}$
$(1,1,1)$	$2.922212\text{ GHz}$	$5.000140\text{ GHz}$
$(2,1,1)$	$4.146842\text{ GHz}$	$6.484398\text{ GHz}$
$(0,1,2)$	$5.982709\text{ GHz}$	$4.776973\text{ GHz}$
$(1,1,2)$	$4.396673\text{ GHz}$	$5.982709\text{ GHz}$
$(2,1,2)$	$5.290341\text{ GHz}$	$7.269033\text{ GHz}$

First, we examine the output of the cavity_pec.json simulation. The file postpro/cavity_pec/eig.csv contains information about the computed eigenfrequencies and associated quality factors:

               m,             Re{f} (GHz),             Im{f} (GHz),                       Q
 1.000000000e+00,        +2.907188343e+00,        +5.814376364e-04,        +2.500000189e+03
 2.000000000e+00,        +2.924244826e+00,        +5.848489468e-04,        +2.500000129e+03
 3.000000000e+00,        +2.924244826e+00,        +5.848489421e-04,        +2.500000149e+03
 4.000000000e+00,        +3.471149740e+00,        +6.942299240e-04,        +2.500000137e+03
 5.000000000e+00,        +4.150836993e+00,        +8.301673534e-04,        +2.500000186e+03
 6.000000000e+00,        +4.150836993e+00,        +8.301673645e-04,        +2.500000153e+03
 7.000000000e+00,        +4.398026458e+00,        +8.796051788e-04,        +2.500000371e+03
 8.000000000e+00,        +4.398026459e+00,        +8.796053549e-04,        +2.499999871e+03
 9.000000000e+00,        +4.632147276e+00,        +9.264294365e-04,        +2.500000101e+03
 1.000000000e+01,        +4.632147278e+00,        +9.264294277e-04,        +2.500000125e+03
 1.100000000e+01,        +4.779153633e+00,        +9.558306713e-04,        +2.500000195e+03
 1.200000000e+01,        +5.005343455e+00,        +1.001068673e-03,        +2.500000096e+03
 1.300000000e+01,        +5.005389580e+00,        +1.001077846e-03,        +2.500000226e+03
 1.400000000e+01,        +5.005389580e+00,        +1.001077950e-03,        +2.499999965e+03
 1.500000000e+01,        +5.293474915e+00,        +1.058694964e-03,        +2.500000094e+03

Indeed we can find a correspondence between the analytic modes predicted and the solutions obtained by Palace. Since the only source of loss in the simulation is the nonzero dielectric loss tangent, we have $Q = Q_d = 1/0.0004 = 2.50\times 10^3$ in all cases.

Next, we run cavity_impedance.json, which adds the surface impedance boundary condition. Examining postpro/cavity_impedance/eig.csv we see that the mode frequencies are roughly unchanged but the quality factors have fallen due to the addition of imperfectly conducting walls to the model:

               m,             Re{f} (GHz),             Im{f} (GHz),                       Q
 1.000000000e+00,        +2.907188345e+00,        +7.091319575e-04,        +2.049821899e+03
 2.000000000e+00,        +2.924244827e+00,        +7.055966146e-04,        +2.072178956e+03
 3.000000000e+00,        +2.924244827e+00,        +7.055966604e-04,        +2.072178821e+03
 4.000000000e+00,        +3.471149742e+00,        +8.644493471e-04,        +2.007723102e+03
 5.000000000e+00,        +4.150836995e+00,        +9.792364835e-04,        +2.119425277e+03
 6.000000000e+00,        +4.150836995e+00,        +9.792365057e-04,        +2.119425229e+03
 7.000000000e+00,        +4.398026451e+00,        +1.000319808e-03,        +2.198310244e+03
 8.000000000e+00,        +4.398026457e+00,        +1.000319601e-03,        +2.198310702e+03
 9.000000000e+00,        +4.632147282e+00,        +1.054123330e-03,        +2.197156287e+03
 1.000000000e+01,        +4.632147282e+00,        +1.054125067e-03,        +2.197152665e+03
 1.100000000e+01,        +4.779153630e+00,        +1.126050842e-03,        +2.122086138e+03
 1.200000000e+01,        +5.005343456e+00,        +1.086214462e-03,        +2.304030995e+03
 1.300000000e+01,        +5.005389584e+00,        +1.171298237e-03,        +2.136684563e+03
 1.400000000e+01,        +5.005389585e+00,        +1.171297627e-03,        +2.136685675e+03
 1.500000000e+01,        +5.293474916e+00,        +1.207733736e-03,        +2.191490929e+03

However, the bulk dielectric loss postprocessing results, computed from the energies written to postpro/cavity_impedance/domain-E.csv, still give $Q_d = 1/0.004 = 2.50\times 10^3$ for every mode as expected.

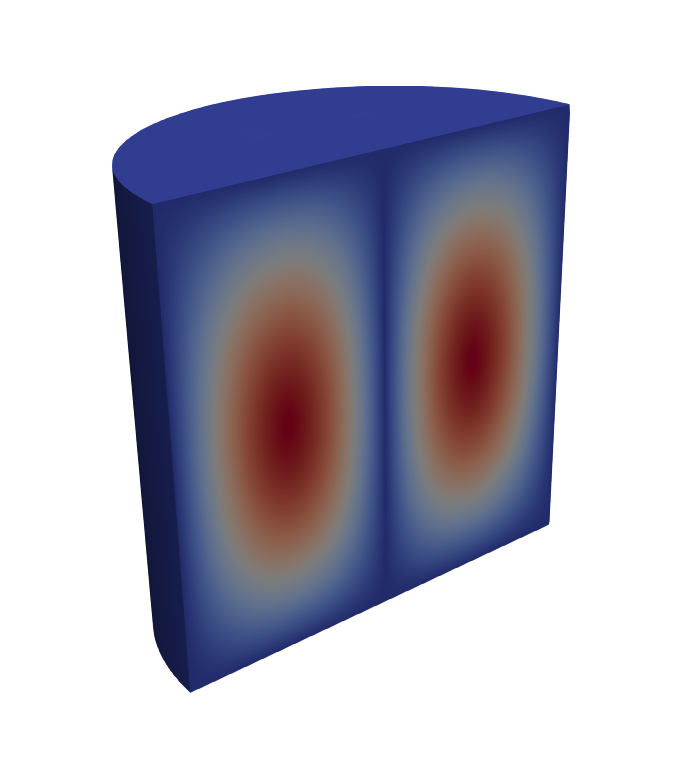
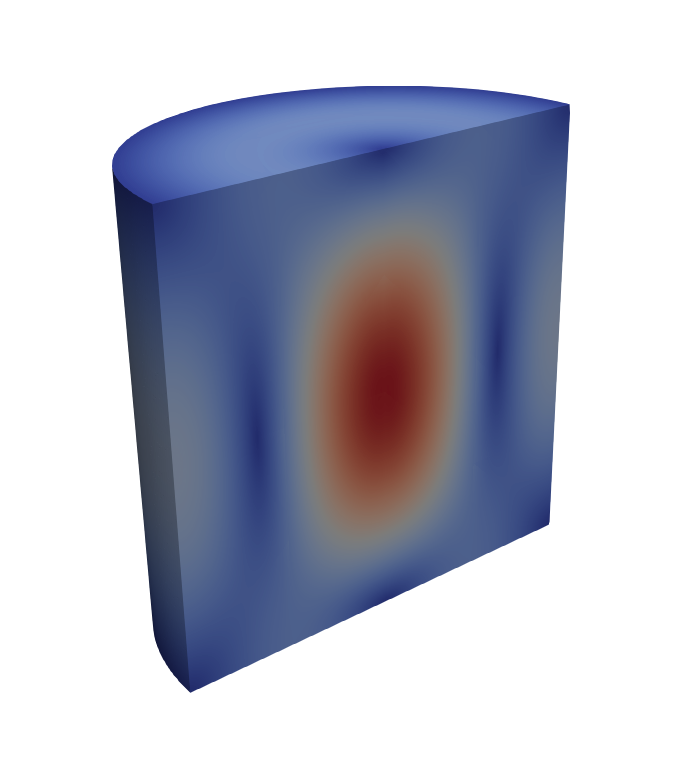
Focusing on the $\text{TE}_{011}$ mode with $f_{\text{TE},010} = 5.00\text{ GHz}$, we can read the mode quality factor $Q = 2.30\times 10^3$. Subtracting out the contribution of dielectric losses, we have

\[Q_c = \left(\frac{1}{Q}-\frac{1}{Q_d}\right)^{-1} = 2.94\times 10^4\]

which is the same as the analytical result given in Example 6.4 from [1] for this geometry.

Finally, a clipped view of the electric field (left) and magnetic flux density magnitudes for the $\text{TE}_{011}$ mode is shown below.

Mesh convergence

The effect of mesh size can be investigated for the cylindrical cavity resonator using convergence_study.jl. For a polynomial order of solution and refinement level, a mesh is generated using Gmsh using polynomials of the same order to resolve the boundary geometry. The eigenvalue problem is then solved for $f_{\text{TM},010}$ and $f_{\text{TE},111}$, and the relative error, $\frac{f-f_{\text{true}}}{f_{\text{true}}}$, of each mode plotted against $\text{DOF}^{-\frac{1}{3}}$, a notional mesh size. Three different element types are considered: tetrahedra, prisms and hexahedra, and the results are plotted below. The $x$-axis is a notional measure of the overall cost of the solve, accounting for polynomial order.

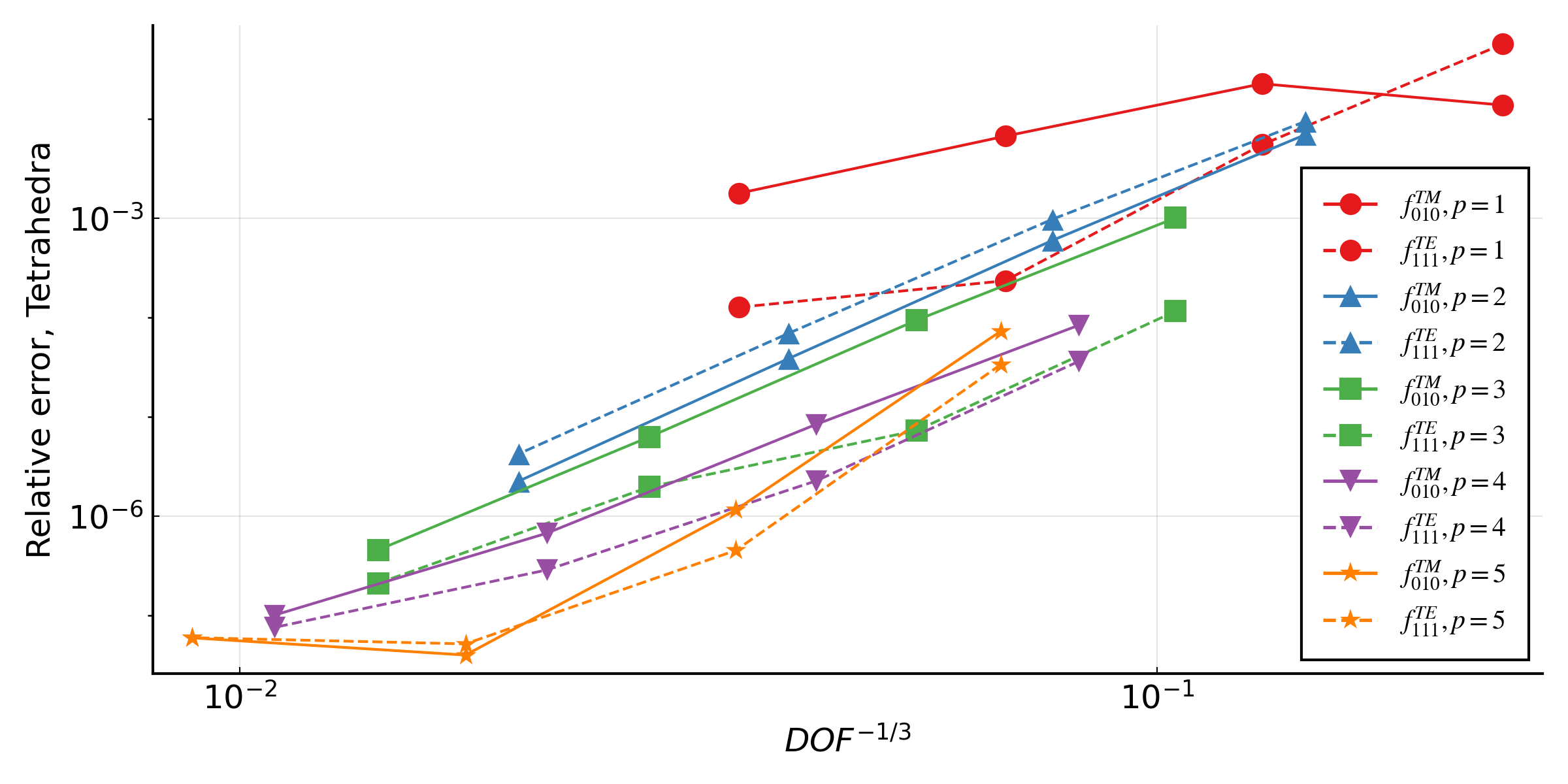
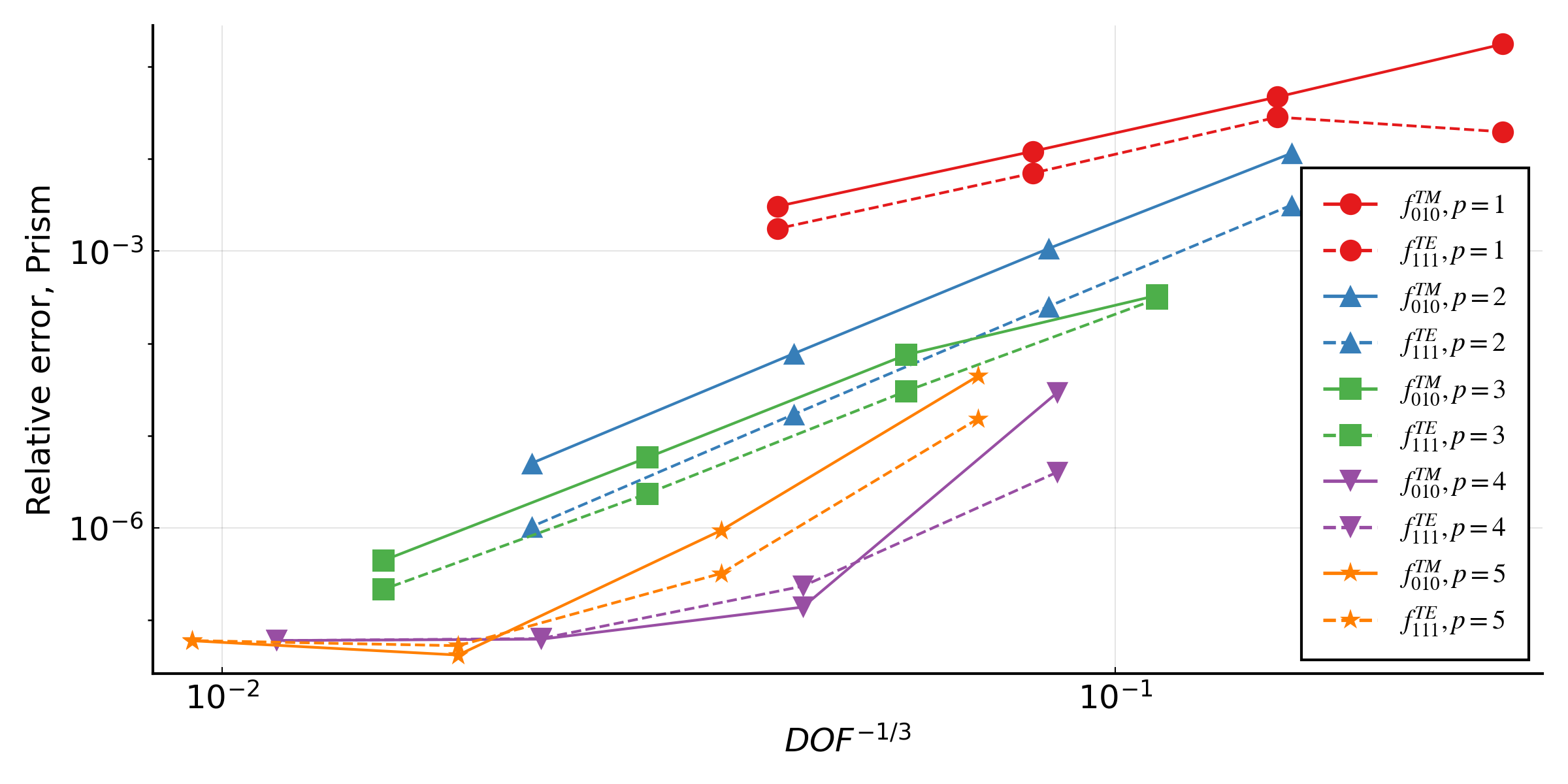
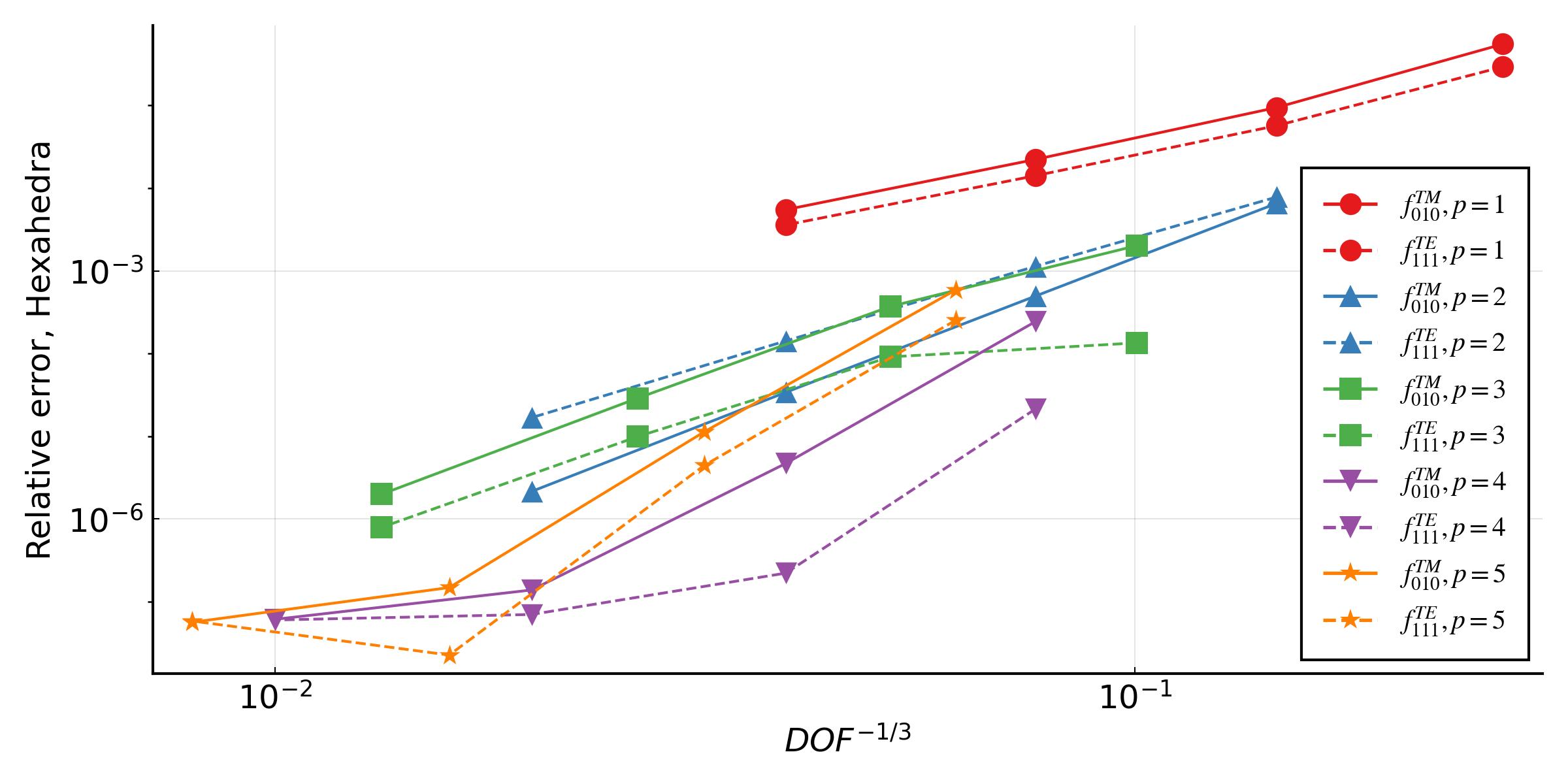
The observed rate of convergence for the eigenvalues are $p+1$ for odd polynomials and $p+2$ for even polynomials. Given the eigenmodes are analytic functions, the theoretical maximum convergence rate is $2p$ [2]. The figures demonstrate that increasing the polynomial order of the solution will give reduced error, however the effect may only become significant on sufficiently refined meshes.

Waveguide

This example demonstrates the eigenmode simulation type in Palace to solve for the cutoff-frequencies of a circular waveguide. As with the cavity the interior material to be Silicon ($\varepsilon_r = 2.08$, $\tan\delta = 4\times 10^{-4}$), with cylindrical domain radius $a = 2.74\text{ cm}$, and length $d=2a = 5.48\text{ cm}$, however now periodic boundary conditions are applied in the $z$-direction. According to [1], the cutoff frequencies for the transverse electric and magnetic modes are given by the formulae:

\[\begin{aligned} f_{\text{TE},nm} &= \frac{1}{2\pi\sqrt{\mu\varepsilon}} \frac{p'_{nm}}{a}\\ f_{\text{TM},nm} &= \frac{1}{2\pi\sqrt{\mu\varepsilon}} \frac{p_{nm}}{a} \end{aligned}\]

which are identical to those for the cavity modes, in the special case of $l=0$.

In addition to these pure waveguide modes, there are aliasing cavity modes corresponding to a full wavelength in the computational domain ($l=2$). In a practical problem these can be suppressed by choosing a smaller value of $d$ which shifts such modes to higher frequencies. The relevant modes are tabulated as

$(n,m,l)$	$f_{\text{TE}}$	$f_{\text{TM}}$
$(0,1,0)$	$4.626481\text{ GHz}$	$2.903636\text{ GHz}$
$(1,1,0)$	$2.223083\text{ GHz}$	$4.626481\text{ GHz}$
$(2,1,0)$	$3.687749\text{ GHz}$	$6.200856\text{ GHz}$
$(3,1,0)$	$5.072602\text{ GHz}$	$7.703539\text{ GHz}$
$(0,1,2)$	$5.982715\text{ GHz}$	$4.776992\text{ GHz}$
$(1,1,2)$	$4.396663\text{ GHz}$	$5.982715\text{ GHz}$
$(2,1,2)$	$5.290372\text{ GHz}$	$7.269056\text{ GHz}$
$(3,1,2)$	$6.334023\text{ GHz}$	$8.586796\text{ GHz}$

For this problem, we use curved tetrahedral elements from the mesh file mesh/cavity_tet.msh, and the configuration file waveguide.json.

The main difference between this configuration file and those used in the cavity example is in the "Boundaries" object: waveguide.json specifies a perfect electric conductor ("PEC") boundary condition for the exterior surface and a periodic boundary condition ("Periodic") on the cross-sections of the cylinder (in the $z-$ direction). The periodic attribute pairs are defined by "DonorAttributes" and "ReceiverAttributes", and the distance between them is given by the "Translation" vector in mesh units.

The file postpro/waveguide/eig.csv contains information about the computed eigenfrequencies and associated quality factors:

               m,             Re{f} (GHz),             Im{f} (GHz),                       Q,
 1.000000000e+00,        +2.223255722e+00,        +4.446511256e-04,        +2.500000155e+03,
 2.000000000e+00,        +2.223255722e+00,        +4.446511297e-04,        +2.500000132e+03,
 3.000000000e+00,        +2.903861940e+00,        +5.807723634e-04,        +2.500000156e+03,
 4.000000000e+00,        +3.688035400e+00,        +7.376066296e-04,        +2.500001577e+03,
 5.000000000e+00,        +3.688035400e+00,        +7.376076214e-04,        +2.499998215e+03,
 6.000000000e+00,        +4.396748739e+00,        +8.793492525e-04,        +2.500001459e+03,
 7.000000000e+00,        +4.396748742e+00,        +8.793504597e-04,        +2.499998028e+03,
 8.000000000e+00,        +4.396843854e+00,        +8.793689551e-04,        +2.499999526e+03,
 9.000000000e+00,        +4.396843859e+00,        +8.793688076e-04,        +2.499999948e+03,
 1.000000000e+01,        +4.626835690e+00,        +9.253659897e-04,        +2.500003152e+03,
 1.100000000e+01,        +4.626835691e+00,        +9.253679806e-04,        +2.499997774e+03,
 1.200000000e+01,        +4.626845256e+00,        +9.253697773e-04,        +2.499998088e+03,
 1.300000000e+01,        +4.777149609e+00,        +9.554297850e-04,        +2.500000408e+03,
 1.400000000e+01,        +4.777237409e+00,        +9.554487274e-04,        +2.499996791e+03,
 1.500000000e+01,        +5.073016463e+00,        +1.014603170e-03,        +2.500000351e+03,
 1.600000000e+01,        +5.073034992e+00,        +1.014607502e-03,        +2.499998810e+03,
 1.700000000e+01,        +5.290571316e+00,        +1.058112715e-03,        +2.500003709e+03,

In common with the PEC cavity $Q = Q_d = 1/0.0004 = 2.50\times 10^3$ in all cases, and all the anticipated waveguide modes are recovered with $\text{TE}_{1,1}$ having the lowest cutoff frequency followed by $\text{TM}_{0,1}$ and $\text{TE}_{2,1}$, while the aliasing mode $\text{TE}_{1,1,2}$ has marginally lower frequency than the waveguide modes $\text{TE}_{0,1}$ and $\text{TM}_{1,1}$ ($4.397\text{ GHz}$ compared to $4.627\text{ GHz}$) and is thus found first.

References

[1] D. M. Pozar, Microwave Engineering, Wiley, Hoboken, NJ, 2012.
[2] A. Buffa, P. Houston, I. Perugia, Discontinuous Galerkin computation of the Maxwell eigenvalues on simplicial meshes, Journal of Computational and Applied Mathematics 204 (2007) 317-333.